2. The modular structure of obscura

The computation of e.g. the electron recoil spectrum probed in direct detection experiments combines inputs from various fields of physics. We need to specify the assumed particle physics of the DM particle. The properties of the DM halo of the Milky way is an important astrophysics input. For the description of the target particles, and how they react to a kick from an incoming DM particle, we need to include knowledge of atomic, nuclear, and condensed matter physics. In order to make predictions, we furthermore need to define the detection experiments specifications. Finally, the result of such an experiment needs to be interpreted using statistics.

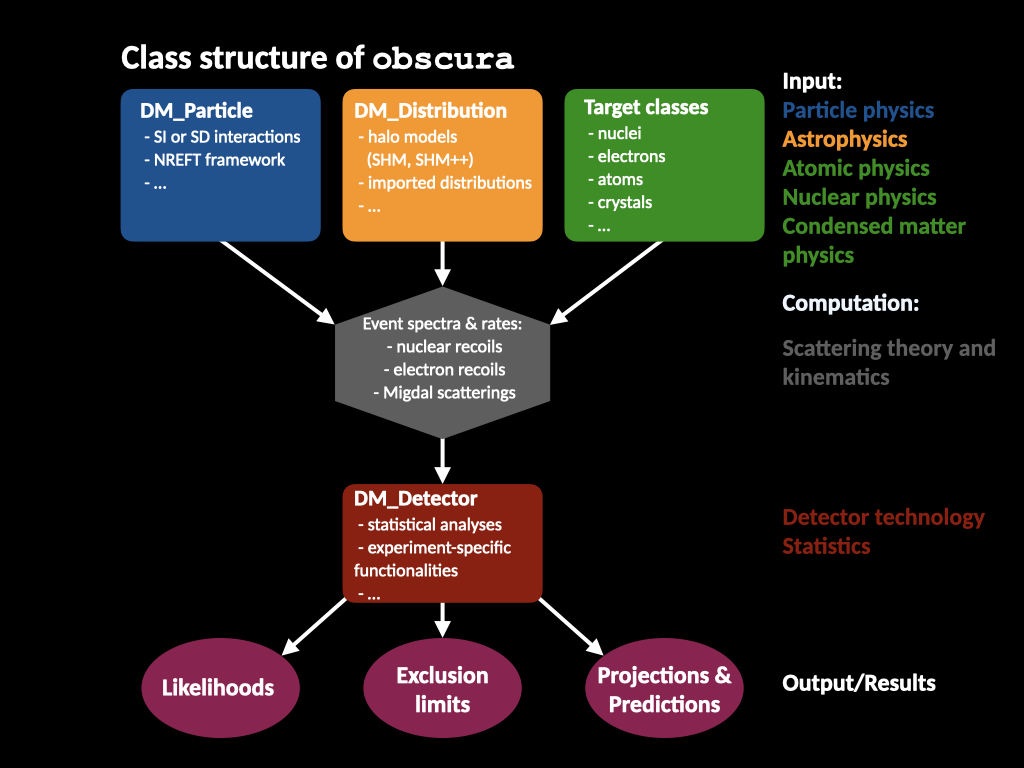
This high level of modularity in this type of calculation needs to be reflected in the code’s polymorphic structure. The goal of obscura is to provide for each of the different inputs one generic interface or abstract base class, that comprises the general required functionalities, without specifying the detailed implementations further. These depend on a multitude of assumptions which can change in different projects, for different users, etc.

If the base classes are defined properly, it is also possible and straight-forward to

1. extend obscura by implementing further derived classes overriding the virtual functions of the base class.

2. design research software that is agnostic to the detailed implementation and thereby very generally applicable to a variety of scenarios. As long as our scientific functions are formulated in terms of these base functions, they will be able to handle any new implementation that comes in the form of derived classes.

The three most important abstract base classes of obscura are

1. DM_Particle

2. DM_Distribution

3. DM_Detector

We will discuss the interface each of these classes provide in more detail. But first we take a look at the detection targets in direct DM search experiments, namely nuclei, bound electrons in atoms, and bound electrons in crystals.